Performs SVD and back substitute to solve equations. More...
#include <TooN/SVD.h>
Public Member Functions | |
| SVD () | |
| SVD (int rows, int cols) | |
| template<int R2, int C2, typename P2 , typename B2 > | |
| SVD (const Matrix< R2, C2, P2, B2 > &m) | |
| template<int R2, int C2, typename P2 , typename B2 > | |
| void | compute (const Matrix< R2, C2, P2, B2 > &m) |
| template<int Rows2, int Cols2, typename P2 , typename B2 > | |
| Matrix< Cols, Cols2, typename Internal::MultiplyType < Precision, P2 >::type > | backsub (const Matrix< Rows2, Cols2, P2, B2 > &rhs, const Precision condition=condition_no) |
| template<int Size, typename P2 , typename B2 > | |
| Vector< Cols, typename Internal::MultiplyType < Precision, P2 >::type > | backsub (const Vector< Size, P2, B2 > &rhs, const Precision condition=condition_no) |
| Matrix< Cols, Rows > | get_pinv (const Precision condition=condition_no) |
| Precision | determinant () |
| int | rank (const Precision condition=condition_no) |
|
Matrix< Rows, Min_Dim, Precision, Reference::RowMajor > | get_U () |
| Vector< Min_Dim, Precision > & | get_diagonal () |
|
Matrix< Min_Dim, Cols, Precision, Reference::RowMajor > | get_VT () |
| void | get_inv_diag (Vector< Min_Dim > &inv_diag, const Precision condition) |
Detailed Description
template<int Rows = Dynamic, int Cols = Rows, typename Precision = DefaultPrecision>
class TooN::SVD< Rows, Cols, Precision >
Performs SVD and back substitute to solve equations.
Singular value decompositions are more robust than LU decompositions in the face of singular or nearly singular matrices. They decompose a matrix (of any shape) 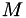 into:
into:
![\[M = U \times D \times V^T\]](form_55.png)
where 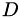 is a diagonal matrix of positive numbers whose dimension is the minimum of the dimensions of
is a diagonal matrix of positive numbers whose dimension is the minimum of the dimensions of 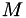 . If
. If 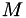 is tall and thin (more rows than columns) then
is tall and thin (more rows than columns) then 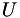 has the same shape as
has the same shape as 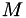 and
and 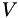 is square (vice-versa if
is square (vice-versa if 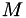 is short and fat). The columns of
is short and fat). The columns of 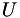 and the rows of
and the rows of 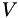 are orthogonal and of unit norm (so one of them lies in SO(N)). The inverse of
are orthogonal and of unit norm (so one of them lies in SO(N)). The inverse of 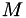 (or pseudo-inverse if
(or pseudo-inverse if 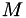 is not square) is then given by
is not square) is then given by
![\[M^{\dagger} = V \times D^{-1} \times U^T\]](form_58.png)
If 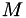 is nearly singular then the diagonal matrix
is nearly singular then the diagonal matrix 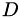 has some small values (relative to its largest value) and these terms dominate
has some small values (relative to its largest value) and these terms dominate 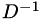 . To deal with this problem, the inverse is conditioned by setting a maximum ratio between the largest and smallest values in
. To deal with this problem, the inverse is conditioned by setting a maximum ratio between the largest and smallest values in 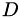 (passed as the
(passed as the condition parameter to the various functions). Any values which are too small are set to zero in the inverse (rather than a large number)
It can be used as follows to solve the 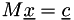 problem as follows:
problem as follows:
// construct M Matrix<3> M; M[0] = makeVector(1,2,3); M[1] = makeVector(4,5,6); M[2] = makeVector(7,8.10); // construct c Vector<3> c; c = 2,3,4; // create the SVD decomposition of M SVD<3> svdM(M); // compute x = M^-1 * c Vector<3> x = svdM.backsub(c);
SVD<> (= SVD<-1>) can be used to create an SVD whose size is determined at run-time.
Constructor & Destructor Documentation
Construct the SVD decomposition of a matrix.
This initialises the class, and performs the decomposition immediately.
Member Function Documentation
| Matrix<Cols,Cols2, typename Internal::MultiplyType<Precision,P2>::type > backsub | ( | const Matrix< Rows2, Cols2, P2, B2 > & | rhs, |
| const Precision | condition = condition_no |
||
| ) |
Calculate result of multiplying the (pseudo-)inverse of M by another matrix.
For a matrix 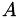 , this calculates
, this calculates 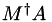 by back substitution (i.e. without explictly calculating the (pseudo-)inverse). See the detailed description for a description of condition variables.
by back substitution (i.e. without explictly calculating the (pseudo-)inverse). See the detailed description for a description of condition variables.
| Vector<Cols, typename Internal::MultiplyType<Precision,P2>::type > backsub | ( | const Vector< Size, P2, B2 > & | rhs, |
| const Precision | condition = condition_no |
||
| ) |
Calculate result of multiplying the (pseudo-)inverse of M by a vector.
For a vector 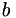 , this calculates
, this calculates 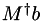 by back substitution (i.e. without explictly calculating the (pseudo-)inverse). See the detailed description for a description of condition variables.
by back substitution (i.e. without explictly calculating the (pseudo-)inverse). See the detailed description for a description of condition variables.
| Matrix<Cols,Rows> get_pinv | ( | const Precision | condition = condition_no | ) |
Calculate (pseudo-)inverse of the matrix.
This is not usually needed: if you need the inverse just to multiply it by a matrix or a vector, use one of the backsub() functions, which will be faster. See the detailed description of the pseudo-inverse and condition variables.
| int rank | ( | const Precision | condition = condition_no | ) |
Calculate the rank of the matrix.
See the detailed description of the pseudo-inverse and condition variables.
| void get_inv_diag | ( | Vector< Min_Dim > & | inv_diag, |
| const Precision | condition | ||
| ) |
Return the pesudo-inverse diagonal.
The reciprocal of the diagonal elements is returned if the elements are well scaled with respect to the largest element, otherwise 0 is returned.
- Parameters:
-
inv_diag Vector in which to return the inverse diagonal. condition Elements must be larger than this factor times the largest diagonal element to be considered well scaled.
Referenced by SVD< Size, Size, Precision >::backsub(), and SVD< Size, Size, Precision >::get_pinv().
 1.7.4
1.7.4