Performs LU decomposition and back substitutes to solve equations. More...
#include <LU.h>
Public Member Functions | |
| template<int S1, int S2, class Base > | |
| LU (const Matrix< S1, S2, Precision, Base > &m) | |
| template<int S1, int S2, class Base > | |
| void | compute (const Matrix< S1, S2, Precision, Base > &m) |
| template<int Rows, int NRHS, class Base > | |
| Matrix< Size, NRHS, Precision > | backsub (const Matrix< Rows, NRHS, Precision, Base > &rhs) |
| template<int Rows, class Base > | |
| Vector< Size, Precision > | backsub (const Vector< Rows, Precision, Base > &rhs) |
| Matrix< Size, Size, Precision > | get_inverse () |
| const Matrix< Size, Size, Precision > & | get_lu () const |
| Precision | determinant () const |
| int | get_info () const |
Detailed Description
template<int Size = -1, class Precision = double>
class TooN::LU< Size, Precision >
Performs LU decomposition and back substitutes to solve equations.
The LU decomposition is the fastest way of solving the equation 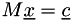 m, but it becomes unstable when
m, but it becomes unstable when 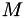 is (nearly) singular (in which cases the SymEigen or SVD decompositions are better). It decomposes a matrix
is (nearly) singular (in which cases the SymEigen or SVD decompositions are better). It decomposes a matrix 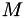 into
into
![\[M = L \times U\]](form_25.png)
where 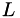 is a lower-diagonal matrix with unit diagonal and
is a lower-diagonal matrix with unit diagonal and 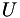 is an upper-diagonal matrix. The library only supports the decomposition of square matrices. It can be used as follows to solve the
is an upper-diagonal matrix. The library only supports the decomposition of square matrices. It can be used as follows to solve the 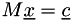 problem as follows:
problem as follows:
// construct M Matrix<3> M; M[0] = makeVector(1,2,3); M[1] = makeVector(3,2,1); M[2] = makeVector(1,0,1); // construct c Vector<3> c = makeVector(2,3,4); // create the LU decomposition of M LU<3> luM(M); // compute x = M^-1 * c Vector<3> x = luM.backsub(c);
The convention LU<> (=LU<-1>) is used to create an LU decomposition whose size is determined at runtime.
Constructor & Destructor Documentation
Construct the LU decomposition of a matrix.
This initialises the class, and performs the decomposition immediately.
References LU< Size, Precision >::compute().
Member Function Documentation
Calculate result of multiplying the inverse of M by another matrix.
For a matrix 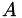 , this calculates
, this calculates 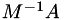 by back substitution (i.e. without explictly calculating the inverse).
by back substitution (i.e. without explictly calculating the inverse).
References Matrix< Rows, Cols, Precision, Layout >::num_cols(), and Matrix< Rows, Cols, Precision, Layout >::num_rows().
Calculate result of multiplying the inverse of M by a vector.
For a vector 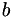 , this calculates
, this calculates 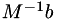 by back substitution (i.e. without explictly calculating the inverse).
by back substitution (i.e. without explictly calculating the inverse).
References Matrix< Rows, Cols, Precision, Layout >::num_rows(), and Vector< Size, Precision, Base >::size().
| Matrix<Size,Size,Precision> get_inverse | ( | ) |
Calculate inverse of the matrix.
This is not usually needed: if you need the inverse just to multiply it by a matrix or a vector, use one of the backsub() functions, which will be faster.
References Matrix< Rows, Cols, Precision, Layout >::num_rows().
| const Matrix<Size,Size,Precision>& get_lu | ( | ) | const |
Returns the L and U matrices.
The permutation matrix is not returned. Since L is lower-triangular (with unit diagonal) and U is upper-triangular, these are returned conflated into one matrix, where the diagonal and above parts of the matrix are U and the below-diagonal part, plus a unit diagonal, are L.
 1.7.4
1.7.4